理解向量
向量具有维度和方向。例如，下图描绘了笛卡尔坐标系中的二维向量 ，表示为箭头。
向量 的头部位于点 。x 坐标值为 ，y 坐标值为 。这些坐标也被称为向量的分量。
相似性
可以使用几种数学公式来确定两个向量是否相似。其中最直观、最容易理解的是余弦相似度。请看下面显示三组图的图片
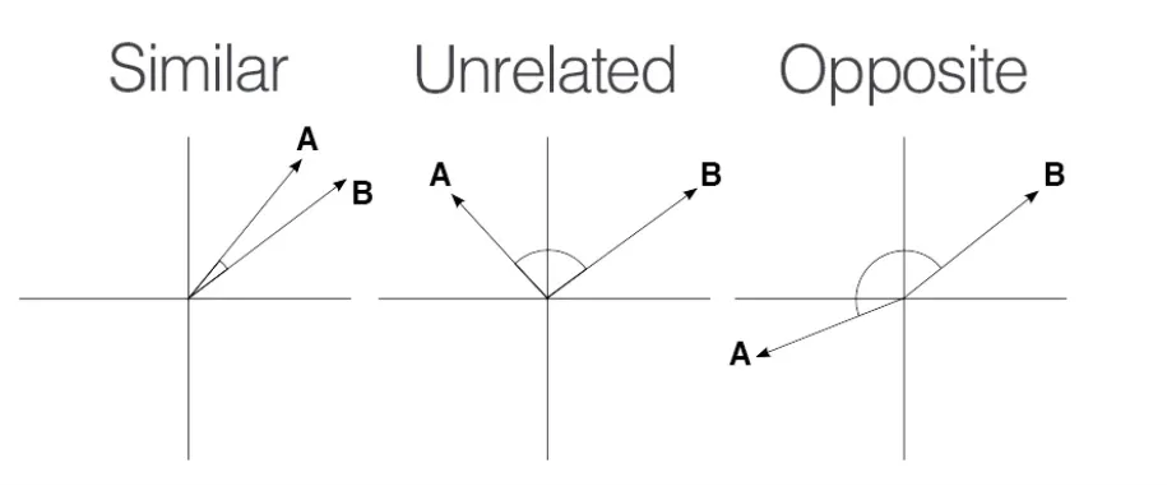
向量 和 在彼此方向接近时被认为是相似的，如第一个图所示。当向量彼此垂直时被认为是无关的，当它们彼此指向相反方向时被认为是相反的。
它们之间的角度 是衡量它们相似性的良好指标。角度 如何计算？
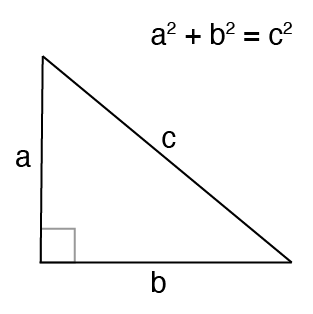
我们都熟悉 勾股定理。
当 a 和 b 之间的角度不是 90 度时，会怎样？
请看 余弦定理。
下图显示了这种方法作为向量图：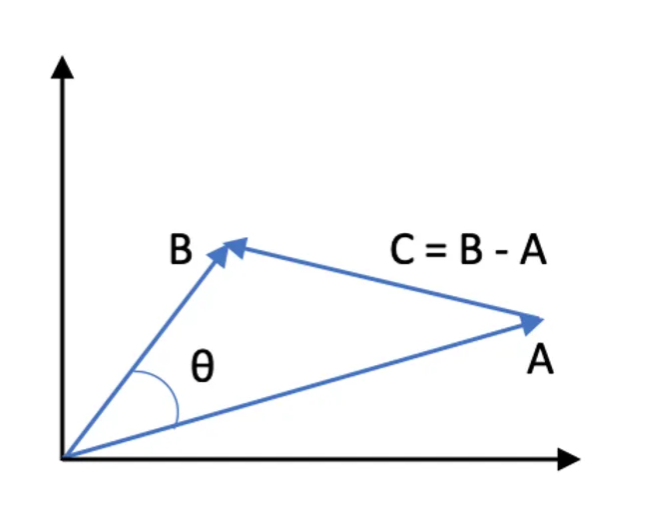
此向量的大小根据其分量定义为
两个向量 和 之间的点积根据其分量定义为
将余弦定理用向量大小和点积重写，得到以下内容
替换 和 得到以下内容
这个公式适用于高于 2 或 3 的维度，尽管很难可视化。然而，它可以在一定程度上可视化。在 AI/ML 应用程序中，向量通常具有数百甚至数千个维度。
使用向量分量在更高维度中的相似性函数如下所示。它通过使用 求和数学语法，将先前给出的二维大小和点积定义扩展到 N 维度。
这是向量存储简单实现中使用的关键公式，可以在 SimpleVectorStore 实现中找到。
